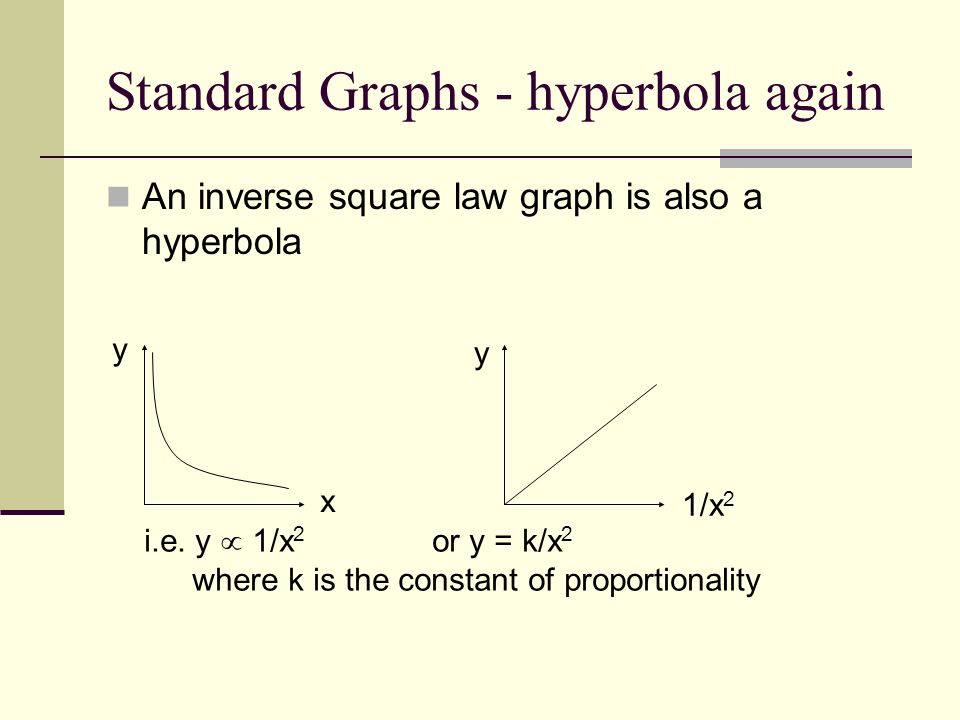
Nonlinear relationship To determine if it is quadratic, calculate the square of the x value and graph the y value vs x2 (This will linearize the data) If the data points then form a line, the model for the original data is quadratic This means that the equation for the original x and y would be y = k • x2 If the data is inverse, itMeans 'y is inversely proportional to the square of x' So y = k ___ x2 where k is a number/constant Substitute, x = 10 and y = 004 into the equation y = k __ x2 Simplify and rearrange to work out the value of k Substitute your value of k into the equation y= __k x 2 Substitute x = 5 into your formula to work out y 1 y is inversely proportional to the square of x A graph demonstrating inverse proportionality of a square function Fig 4 above shows a graph where the values on the y axis go down in inverse proportion to the squares of the values on the x axis ie y ∝ 1/x2 or y = k/x2 where k is a constant
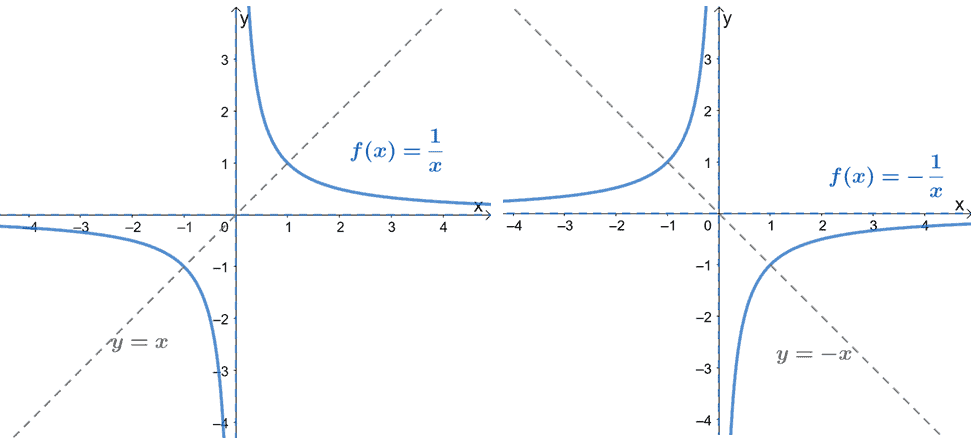
Reciprocal Function Properties Graph And Examples
Inverse square y=k/x^2 graph
Inverse square y=k/x^2 graph- The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bx c Our job is to find the values of a, b and c after first observing the graphGraphing Transformations Of Reciprocal Function Example Given the function y = − 2 3 ( x − 4) 1 a) Determine the parent function b) State the argument c) Rearrange the argument if necessary to determine and the values of k and d d) Rearrange the function equation if necessary to determine the values of a and c




Graph Of Y K X 2 Novocom Top
A region R is enclosed by the coordinate axes and the graph of y = k (x — 5)2, k > 0 When this If f (x) = x 3, what is the derivative of the inverse of f (x) ?Question If y varies inversely as the square of x and y=9 when x=2, write the equation of variation and find the value of x when y=4 Answer by ewatrrr() (Show Source) A 0 the range is y k X 2 6x 16 0 2x 2 11x 12 0 x 2 4 0 x 2 3x 2 0 etc Lets determine the continuity intervals we are going to look for the intervals of the function fx 1 A quadratic inequality is an equation of second degree that uses an inequality sign instead of an equal sign
Inverse proportion worksheet 1 offers a step by step process finding the constant k when k is positive Inverse proportion worksheet 2 contains sketching graphs questions and answers Inverse proportion worksheet 3 offers more advanced problems involving x squared, x cubed and the square and cube root of xSince this graph is not a straight line, the relationship is not just inverse, but rather inverse square or inverse cube The next logical step is to plot y versus 1/x2 (inverse square) The plot of this graph is shown below The line still is not straight, so the relationship is not inverse square Finally, try a plot of y versus 1/x3 Aha! Find the area and perimeter of each composite figure use 314 for π round your answer to the nearest tenth a square and a right triangle share a common side image long description a 3meter by 05meter rectangle has triangles attached like wings to the 3meter sides the other two sides of both triangles measure 25 meters the height of each triangle is 2
When the graph of a function is changed in appearance and/or location we call it a transformation There are two types of transformations Compare the graph of g and h to the basic square root function defined by f (x) = x, Use different colors to graph the family of graphs defined by y = k xInclude a screenshot of the graph in your portfolio and explain its significance I used the National Debt database from 1930 to 1985 created a new field (years since 1930), The function graphed is of the form y = k/x^2 (by the inverse square law) What is the valueAnswer to If y varies inversely as the square of x, and y = 05 when x = 1, find y when x = 9 By signing up, you'll get thousands of stepbystep




2 Use Table 2 To Solve Problems 2a 2c A Create A Chegg Com
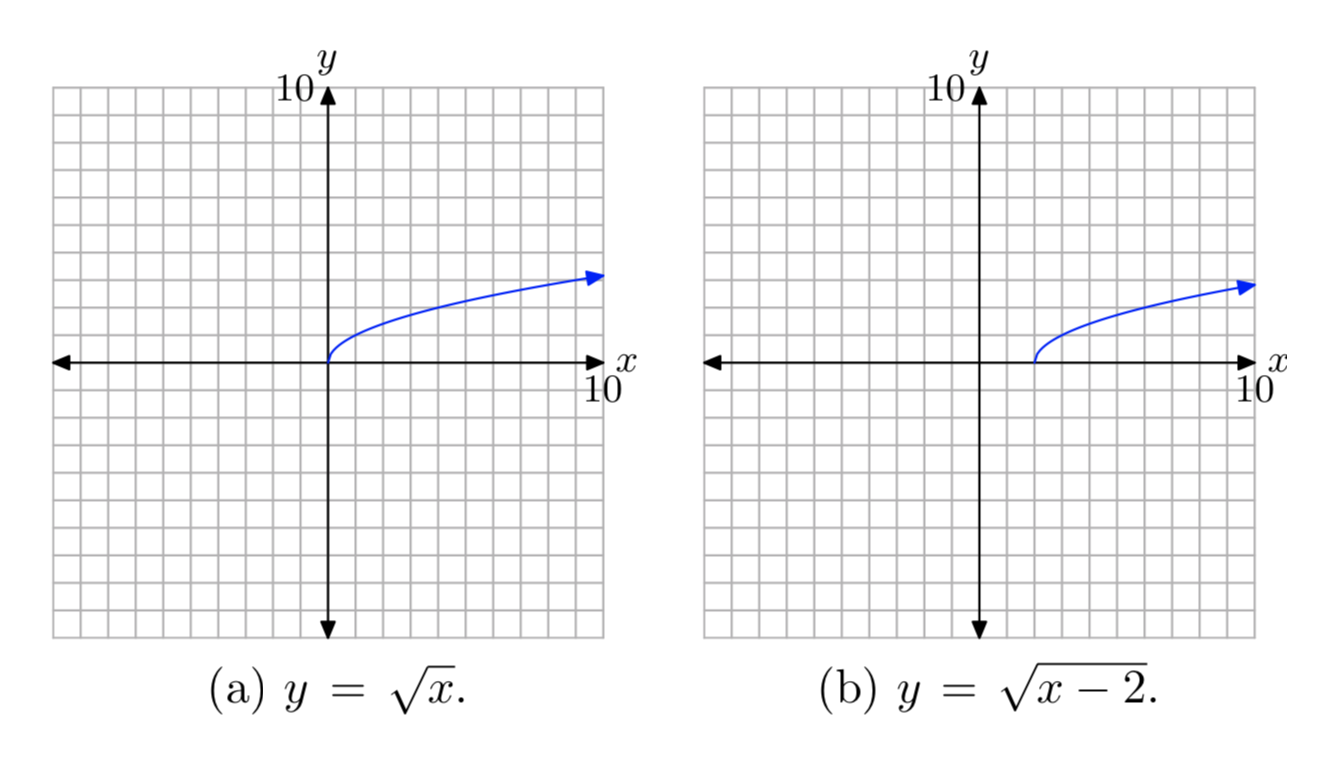



9 1 The Square Root Function Mathematics Libretexts
Y varies exponentially with x Thus y might vary with the square of x or the cube of x The next logical plot would be y versus x2 The graph looks like this y x2 Since this plot is a straight line passing through the origin, y varies with the square of x, and the equation is y = k•x2F varies jointly with m 1 and m 2 and inversely with the square of d Mixed Examples If y varies directly as the square of x when y=3 and x=2, find y when x=1 y = k x 2 3 = k (2) 2 3 / 4 = k The graph is curved meaning it is INVERSESince this plot is a straight line passingthrough the origin, y varies with the square of x, and the equationis y = k•x2 Again, place yon one side ofthe equation and x2on the other, multiplying x2by the proportionality constant,k Determine kby dividingy by x2 k= y/x2= 8/(2)2= 8/4 = 2




Reciprocal Functions Definition Examples Graphs Video Lesson Transcript Study Com
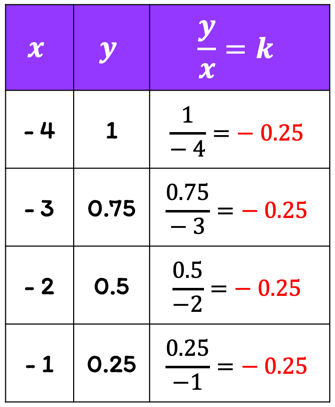



Direct Variation Chilimath
Formula y varies inversely as the square of x y = k/x^2 (k is the constant ofIn some situations, one variable varies directly with the square of the other variable When that happens, the equation of direct variation is y = k x 2 y = k x 2 We solve these applications just as we did the previous ones, by substituting the given values into the equation to solve for kAn inversesquare relationship is another relationship between $y$ and $x$ It is not symmetrical So if $y=k/x^2$, then $x = \sqrt{k}/\sqrt{y}$, hence the connection the the square root function Let us assume $y = k/(x^2)$ If $x$ is multiplied by $t$, then $y$ is affected by a factor of $1/t^2$



Graphing Logarithmic Functions



6 4 Onto Functions Mathematics Libretexts
(D) —3x Answer 25 If fis a differentiable function on the closed interval a, b, which of the following theorems fully square centimeters per second, is the surface areaK 44 Unit 6 Direct and inverse proportion Practise the methods Answer this question to check where to start 1 Match each proportionality statement with an equation A y is directly proportional to x i y = k __ x B y is inversely proportional to x ii y = k x 2 C y is directly proportional to the square of x iii y = k __ x 2 D y is inversely proportional to the square of xSince this plot is a straight line passing through the origin, y varies with the square of x, and the equation is y = k•x2 Again, place y on one side of the equation and x2 on the other, multiplying x2 by the proportionality constant, k Determine k by dividing y by x2 k = y/x2 = 8/(2)2 = 8/4 = 2
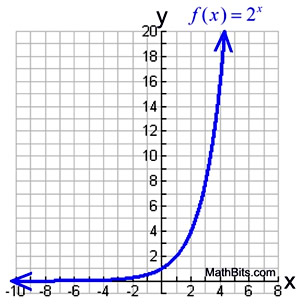



Exponential Functions Mathbitsnotebook Ccss Math




The Characteristics Of The Graph Of A Reciprocal Function Graphs And Functions And Simultaneous Equations
Graph is an upward curve Taking the square of the control, you get a straight line graph Ratio of Dependent/(Control 2) is a constant value For a square relationship, when we double the value of the control variable, the dependent variable becomes four times larger When the control is tripled, the dependent becomes nine times largerGraphs Sketch the shapes of the following graphs y=mxc Direct proportion Inverse proportion y=k/x Inverse square law y=k/x2 Square relationship y = kx2 Y=ksinx Explain using a diagram how to find the gradient of a straight line graph Describe how you could extend this method to find the gradient of a curveInverse square relationship, y 1/x2 or y = k/x2 The relationship between x and y resembles the graph of y = 1/x2 for positive x The intensity of a lighthouse beam is measured at various distances from the source, and the following results obtained, taking the relative intensity at 5 km as 100
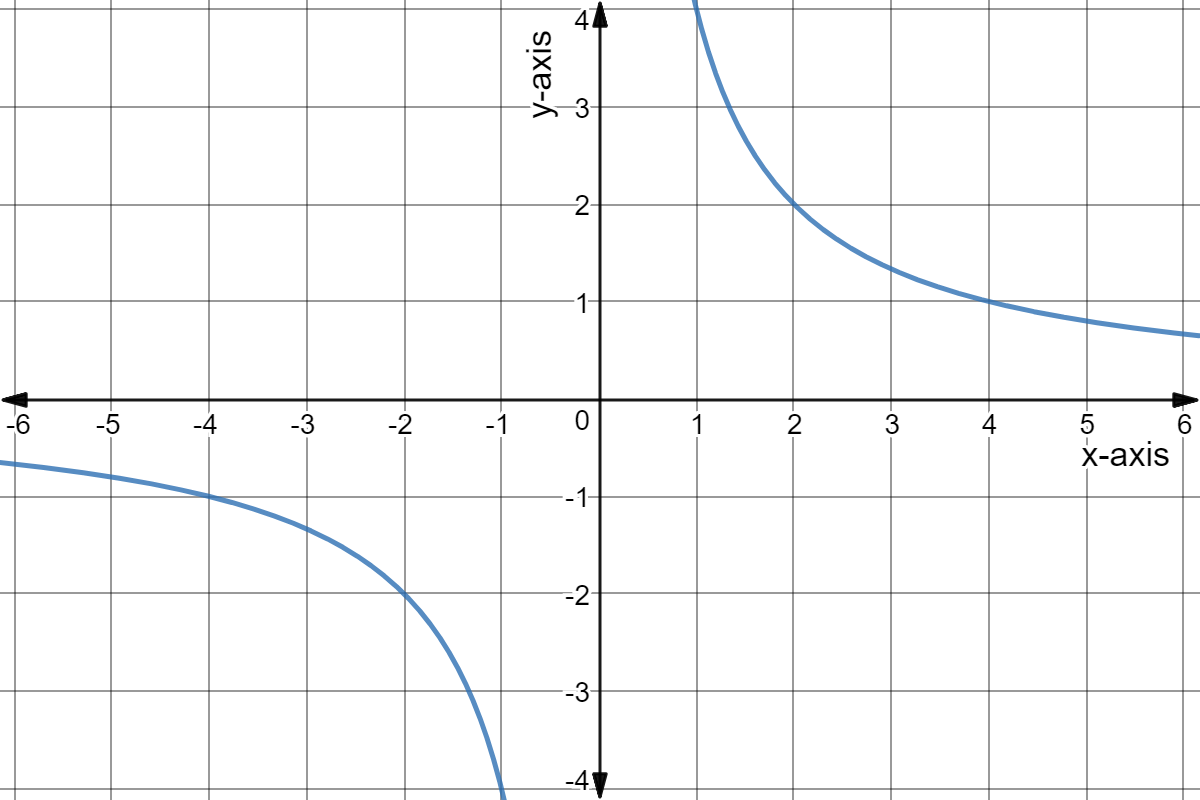



Inversely Proportional Functions In Depth Expii
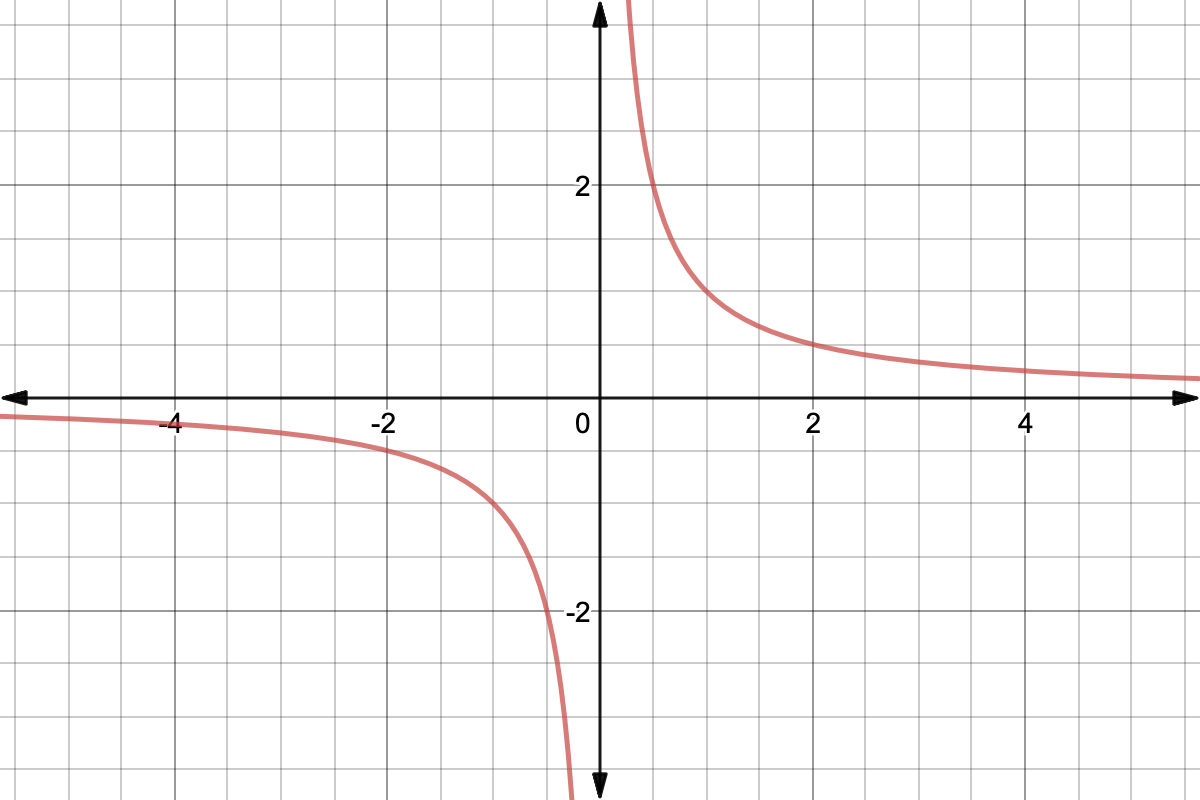



Inversely Proportional Functions In Depth Expii
By the quadratic formula Completing the square, which is often done to find the vertex and axis of symmetry anyway, is often the most efficient way of laying bare all of the features of the parabola For example, to analyse the graph of the quadratic function y = x 2 4 x − 5, we complete the squareFree functions inverse calculator find functions inverse stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyNC Math 2 Unit 6 Square Root and Inverse Variation Functions y=k·x2, where k is a negative number In this unit, you have been introduced to two new types of functions the square root function and the inverse variation function Each of these functions also has a parent graph Square root function parent graph y=√x



File Inverse Square Graph Svg Wikimedia Commons



Inverse Relationships
Special Case Direct Square variation \(y=k{{x}^{2}}\) Here is a sample graph for inverse or indirect variation This is actually a type of Rational Function (function with a variable in the denominator) that we will talk about in the Rational Functions, Equations and Gravity follows the inversesquare law, which means that as you double the distance, the force of gravity becomes onefourth as strong Duration 251 y=4/(3x^2) Since y varies inversely with the square of x, y prop 1/x^2, or y=k/x^2 where k is a constant Since y=1/3ifx=2, 1/3=k/(2)^2 Solving for k gives 4/3 Thus, we can express y in terms of x as y=4/(3x^2)
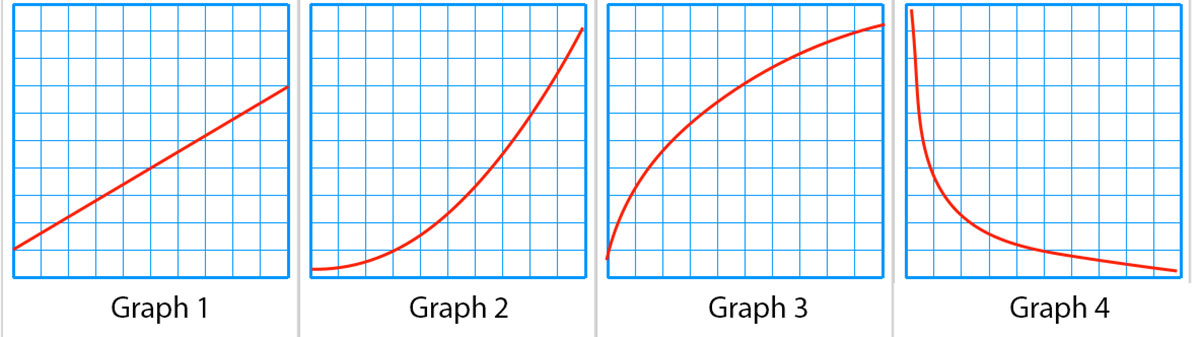



Mathematical Relationships Mathematical Relationships



1
The notes introduce hyperbolas and inverse square functions The impact of the constant (k) is explored as are asymptotes and discontinuous graphsInverse proportion Two quantities are in inverse proportion when as one variable increases, the other decreases at the same rate and vice versa You write y is inversely proportional to x as y ∝ 1 x or y = k When k is positive, the graph y = k x has a similarSquare vertical parabola with vertex at the origin 3 y = kx 3 cube −1 y = k/x inverse rectangular hyperbola −2 y = k/x 2 inverse square −3 y = k/x 3 inverse cube ½ y = k√x square root horizontal parabola with vertex at the origin ⅓ y = k∛x cube root




Graph Of Y K X 2 Novocom Top



Math Scene Functions 2 Lesson 6 Inverse Functions
Example 2 Find the inverse function, if it exists State its domain and range This function is the "bottom half" of a parabola because the square root function is negative That negative symbol is just − 1 1 −1 in disguise In solving the equation, squaring80 Variation and Graphs Chapter 2 For the inversevariation function with equation y = __k xn, we say y varies inversely as xn, or y is inversely proportional to xn In an inverse variation, as either quantity increases, the other decreases In the painting example, as the number of workers increases, the number of hours each must work decreasesBy completing the square;
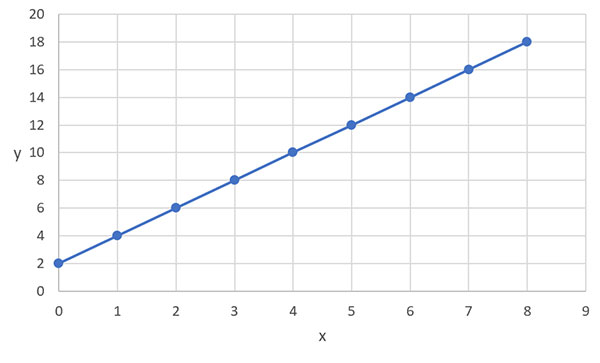



Mathematical Relationships Mathematical Relationships



2fv5d843v9w22sxtto1ibxtu Wpengine Netdna Ssl Com Wp Content Uploads 15 12 Ratio H Direct Inverse Proportion V2 Solutions Pdf
A Two quantities are said to be proportional if a change in one is always accompanied by a change in the other, and if the changes are always related by use of a constant multiplier The constant is called the coefficient of proportionality or y=36 y varies inversely as the square of x means y=k/x^2 Solving for k k=x^2y k=(6)^2(4) k= To find y when x=2, we go back to the orinal equation y=k/(2)^2 y=(6)^2(4)/4 y=36Question If y varies inversely as the square of x and y = 4 when x = 3, find y when x is 2 Answer by Cromlix (4381) ( Show Source ) You can put this solution on YOUR website!
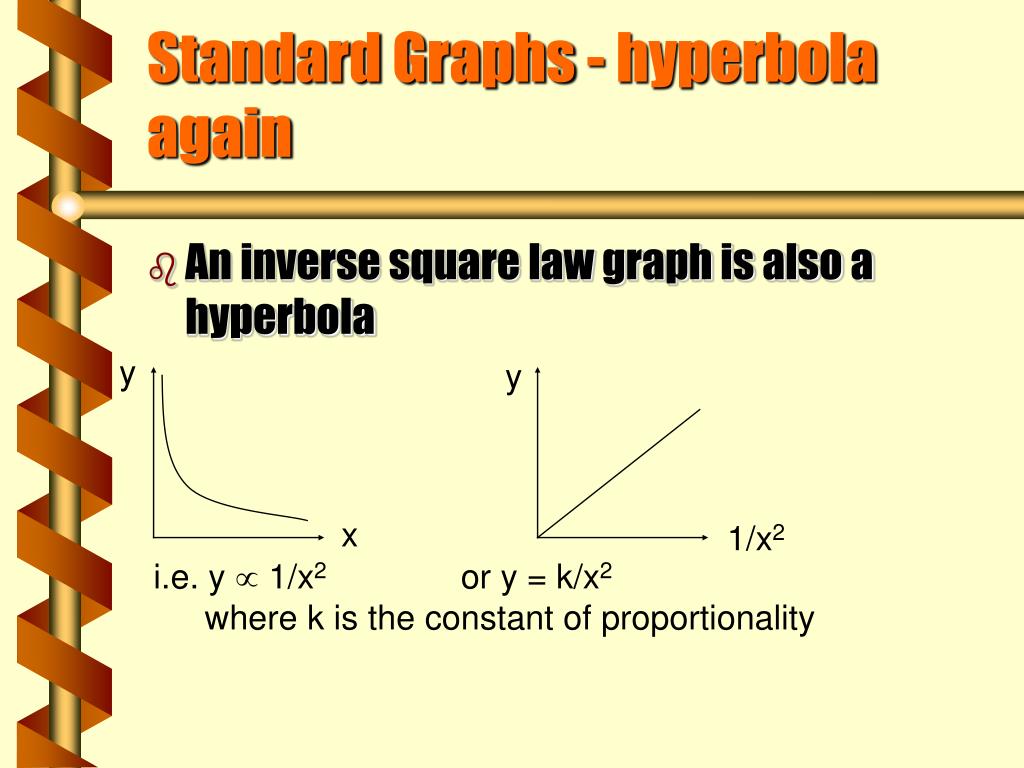



Ppt Physics And Physical Measurement Powerpoint Presentation Free Download Id




Recognizing Direct Inverse Variation Table Video Khan Academy
The graph of y against x n is a straight line passing through the origin 3 It is given that P varies directly as the square of Q and inversely as the square root of R Given that the constant is k, find the relation between P, Q and R y ∝ 1 x 2 → y = k x 2 3 = k 6 2 k = 3Draw a graph by completing the table of values 1 As \(\text {y}\) is inversely proportional to \(\text {x}\) we can write \\text {y = k / x}\ 2 Inverse variation If x and y are two variables, then the direct variation is y = kx, where, k is some nonzero constant If x and y are two variables, then the inverse variation is y = k / x , where, k is some nonzero constant The non zero constant k is called the constant of variation, and y is said to vary inversely with x Observe the equations for the relationships
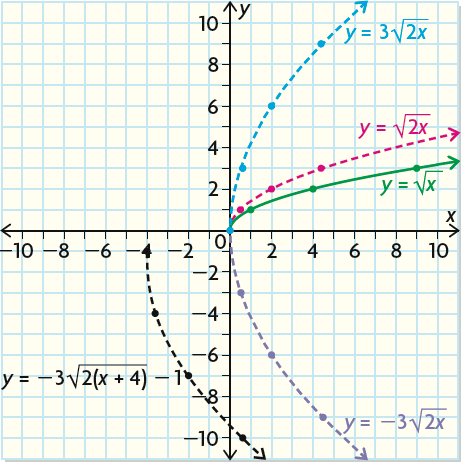



Using Transformations To Graph Functions Of The Form




Direct Variation Free Math Help
Start studying Physics Graphing Learn vocabulary, terms, and more with flashcards, games, and other study tools direct square relationship y=kx^2 inverse relationship as x increases y decrease y=k/x inverse square relationship field and distance (?) y=k/x^2 best fit "line" (curve) average of data *do not connect the dots like youAcademiaedu is a platform for academics to share research papersNC Math 2 Unit 6 Square Root and Inverse Variation Functions , where k is a negative number y = k x 2 In this unit, you have been introduced to two new types of functions the square root function and the inverse variation function Each of these functions also has a parent graph Square root function parent graph y = √ x Inverse variation function parent graph y = x 1
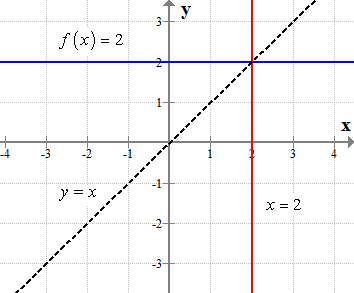



Inverse Of Constant Function Chilimath
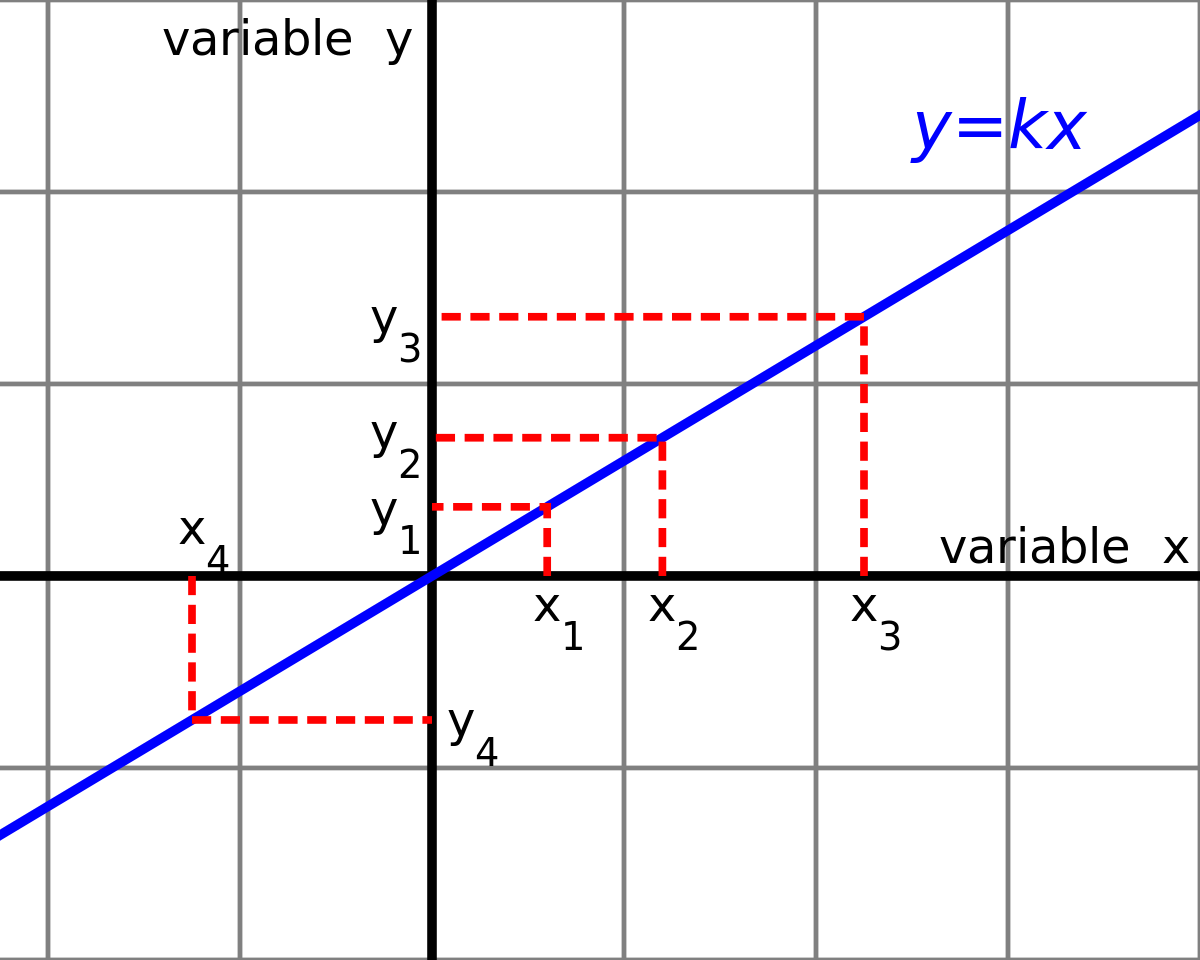



Proportionality Mathematics Wikipedia
Square vertical parabola with vertex at the origin 3 y = kx 3 cube −1 y = k/x inverse rectangular hyperbola −2 y = k/x 2 inverse square −3 y = k/x 3 inverse cube ½ y = k√x square root horizontal parabola with vertex at the origin ⅓ y = k∛x cube rootY=k·x2, where k is a negative number In this unit, you have been introduced to two new types of functions the square root function and the inverse variation function Each of these functions also has a parent graph Square root function parent graph y=√x Inverse variation function parent graphDetermine k by dividing y by x 2 k = y/x 2 = 8/(2) 2 = 8/4 = 2 This value will be the same for any of the four ordered pairs, and yields the equation y = 2 • x 2 (y varies directly with the square of x) EXAMPLE 3 x y 2 24 3 16 4 12 8 6 12 4 A plot of y versus x gives a graph that looks like this y x A graph with this curve always suggests an inverse relationship
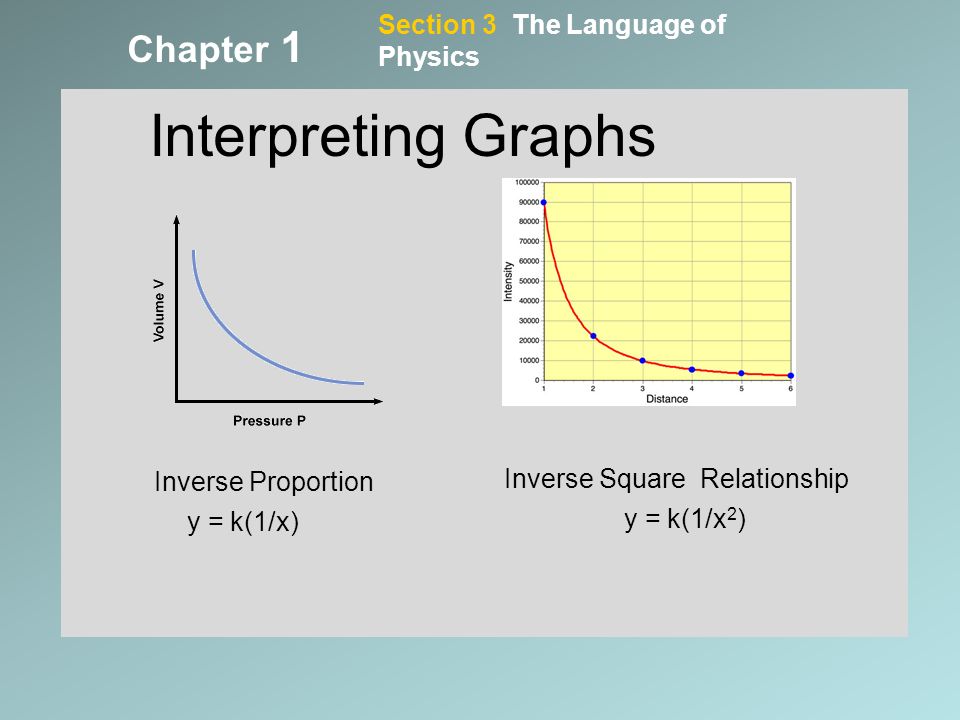



The Science Of Physics Chapter 1 Holt 1 1 What Is Physics Physics Is The Scientific Study Of Matter And Energy And How They Interact With Each Other Matter Ppt Download



All Elementary Mathematics Study Guide Functions And Graphs Elementary Functions And Their Graphs
The rules from graph translations are used to sketch the derived, inverse or other related functions Complete the square to find turning points and find expression for composite functions
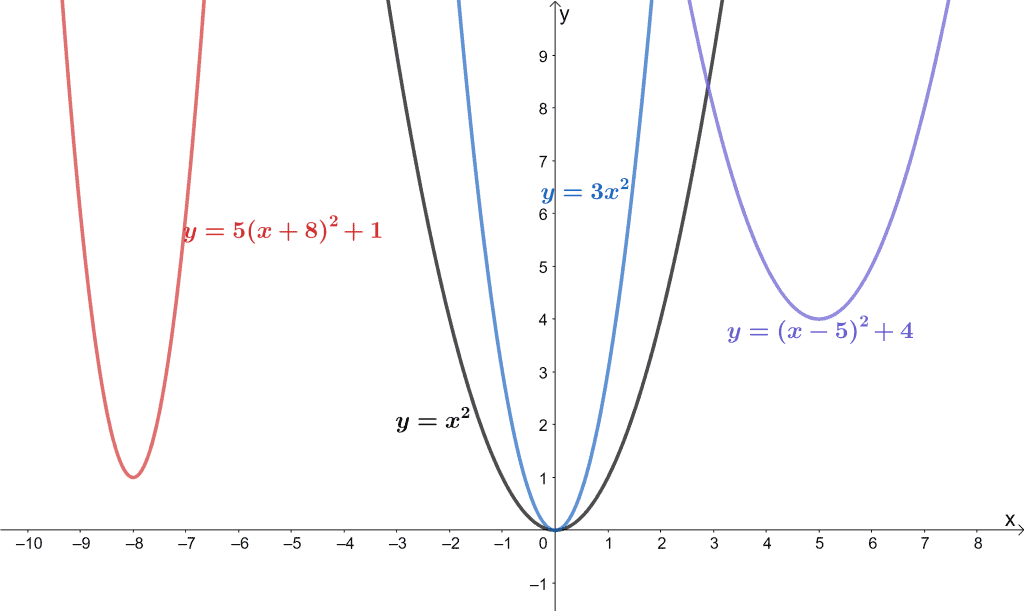



Parent Functions Types Properties Examples




Direct And Inversely Proportional Quantities Concepts Videos Examples




Proportionality Mathematics Wikipedia




Sketch And Interpret Graphs Of Reciprocal Functions Y K X 2 Youtube
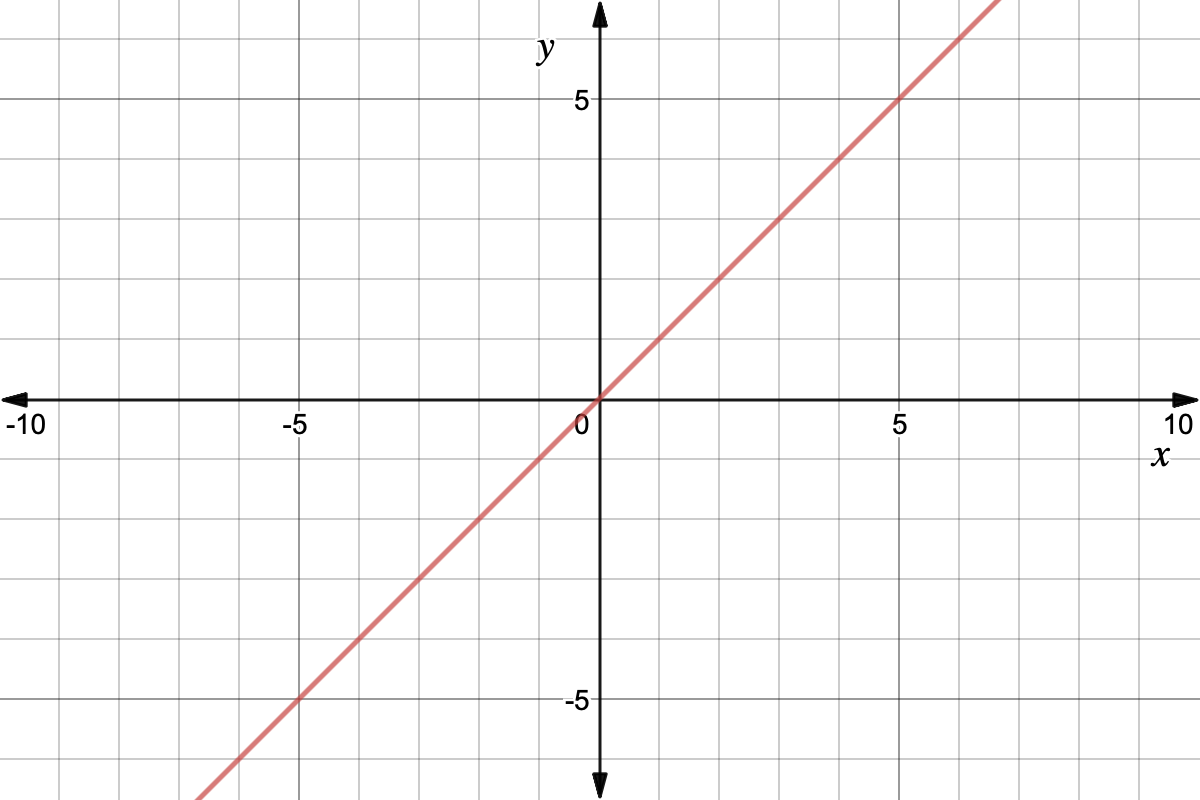



Directly Proportional Functions In Depth Expii
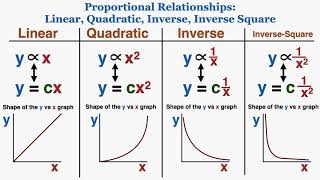



Using Linear Quadratic Inverse Inverse Square Graphs To Understand Proportionality Ib Physics Youtube



Http Www Mpsaz Org Rmhs Staff Lxcoleman Trig Test Practice Files Review Chapter 3 Notes Solutions Pdf



Solution In A Quadratic Variation Graph What Does It Look Like When Y Equals 18 When X Equals 6 What Does The Rest Of The Graph Look Like
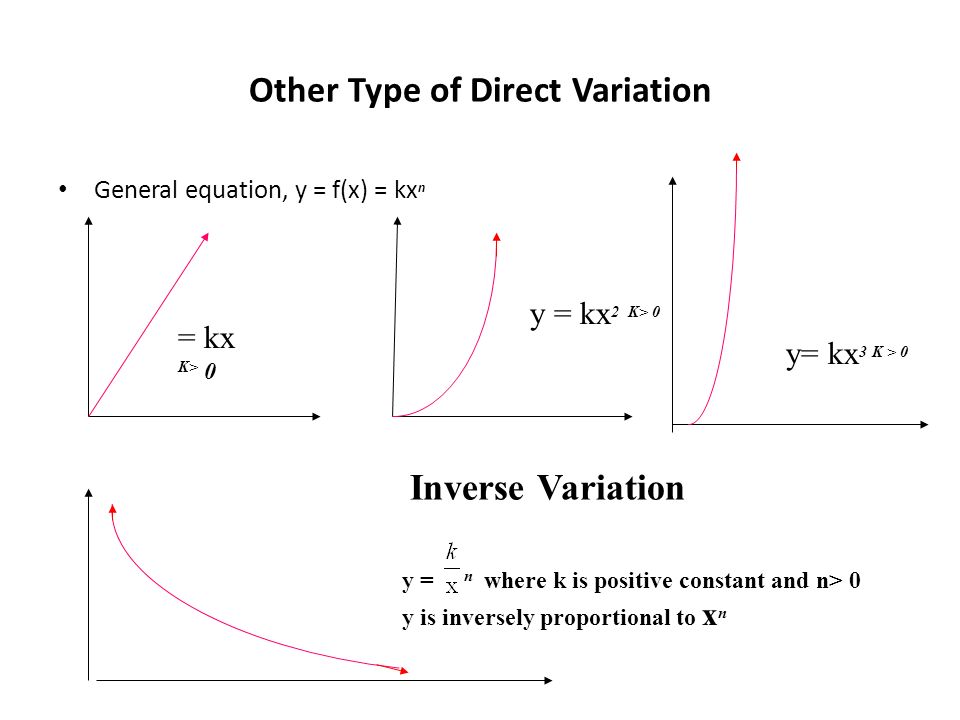



Chapter 3 1 Variation Ppt Video Online Download



Inverse Relationships
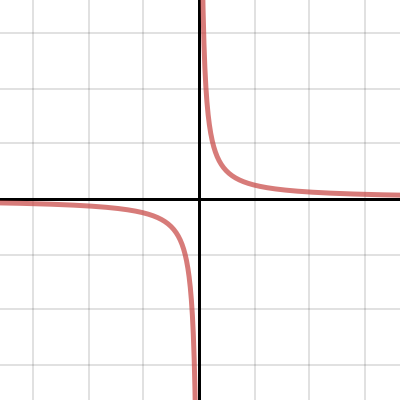



Explore Y K X Inverse Variation



Does The Graph Of K Xy Represent A Function Quora




Pplato Flap Phys 1 3 Graphs And Measurements




Lesson 12 1 Inverse Variation Objectives Graph Inverse



What Are The Characteristics Of Direct Proportionality Relationship Graph Quora



Group Activity Graphing Direct And Inverse Proportions
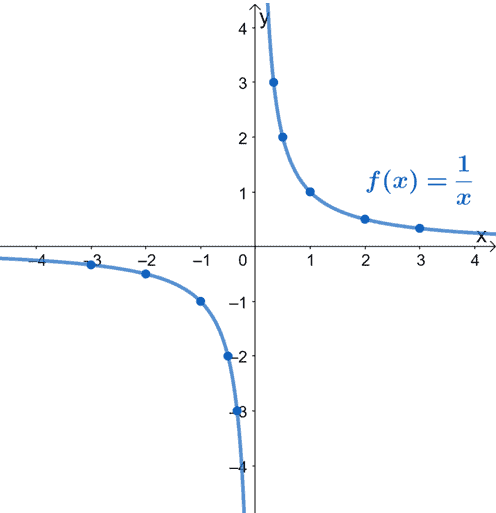



Reciprocal Function Properties Graph And Examples



Exponetials And Growth Functions
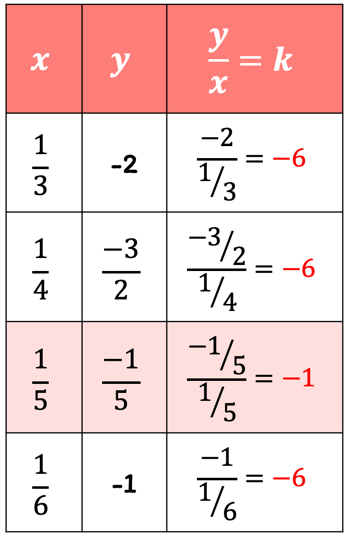



Direct Variation Chilimath
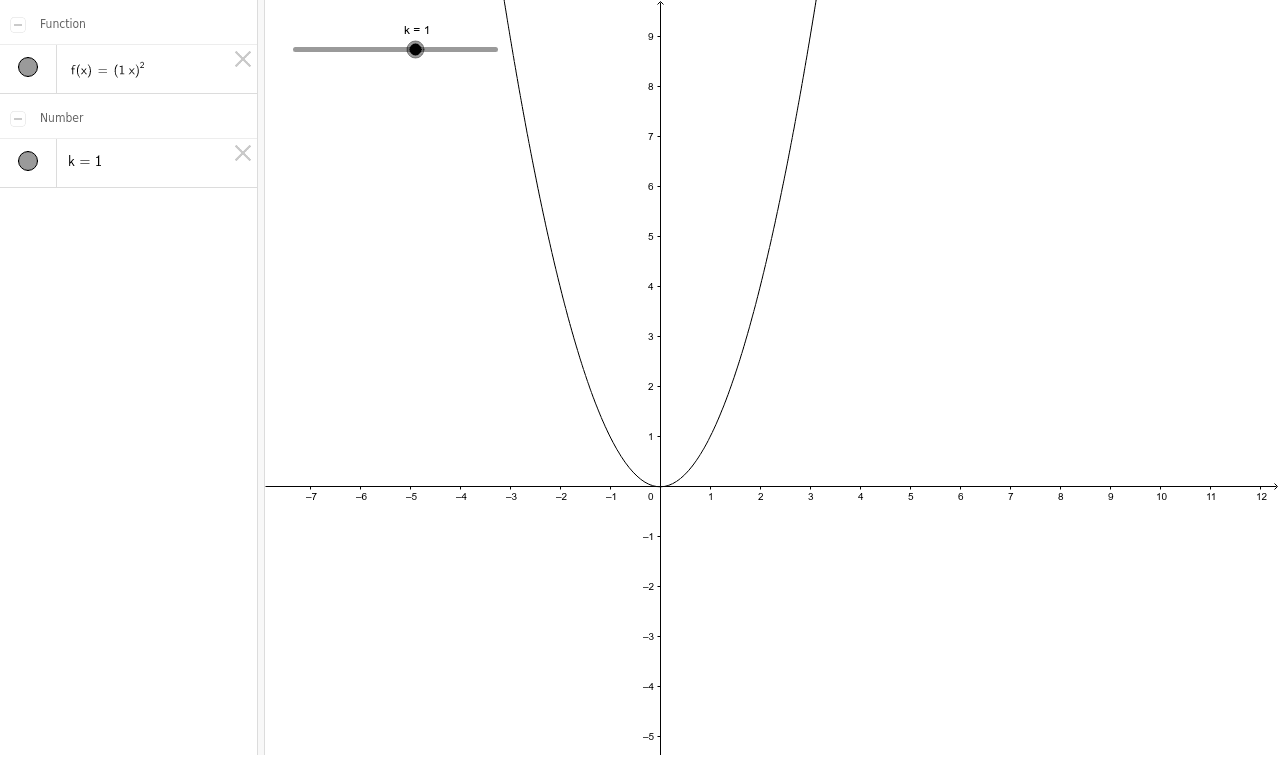



Describing Variation Graphs Station 2 The Graph Of Y Kx 2 Geogebra
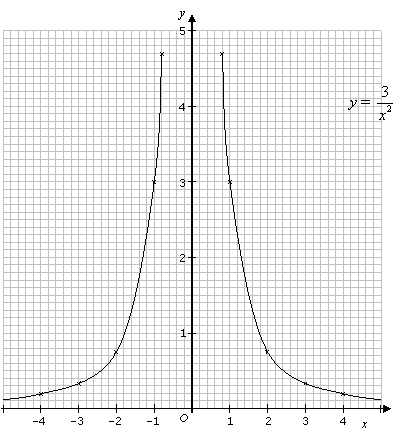



Graphs Of Reciprocal Functions Video Lessons Examples And Solutions



Drawing Trigonometric Graphs The Basic Graphs You Should



Physics And Physical Measurement Topic 1 2 Measurement And Uncertainties Ppt Download



Ex 1 Graph A Direct Variation Equation Positive Slope Youtube
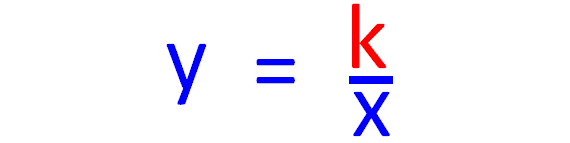



Constant Of Proportionality
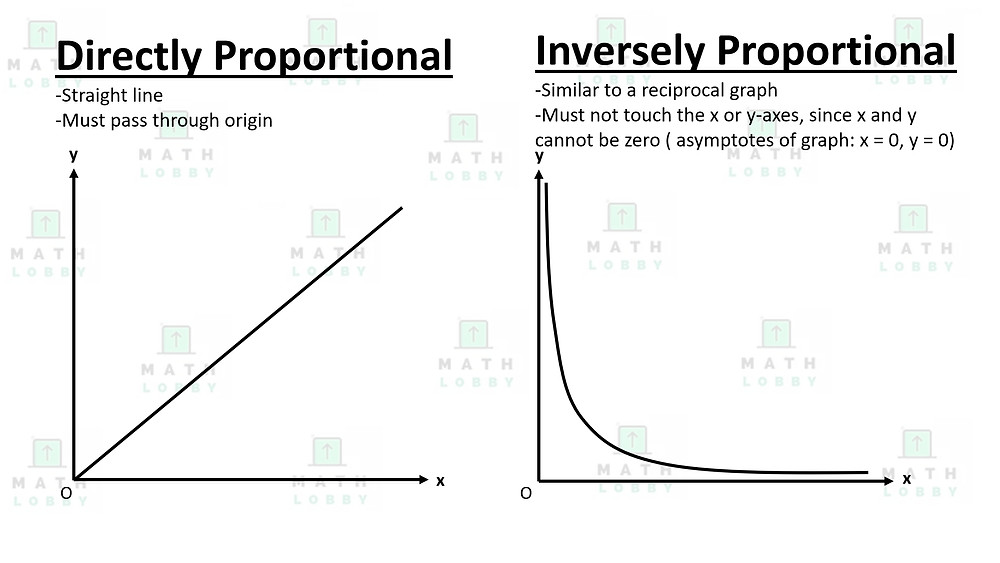



Direct And Inverse Proportion
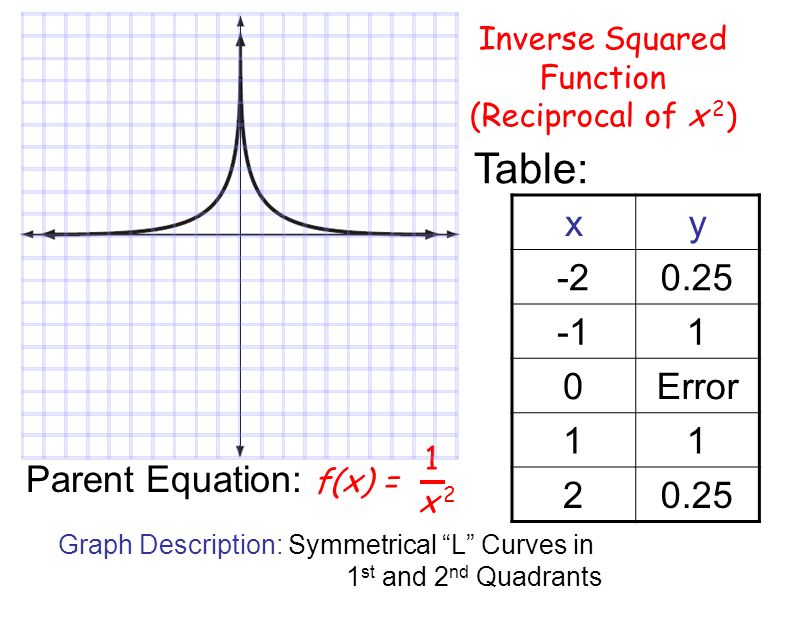



Parent Functions Constant Function Linear Identity Absolute Value Ppt Video Online Download
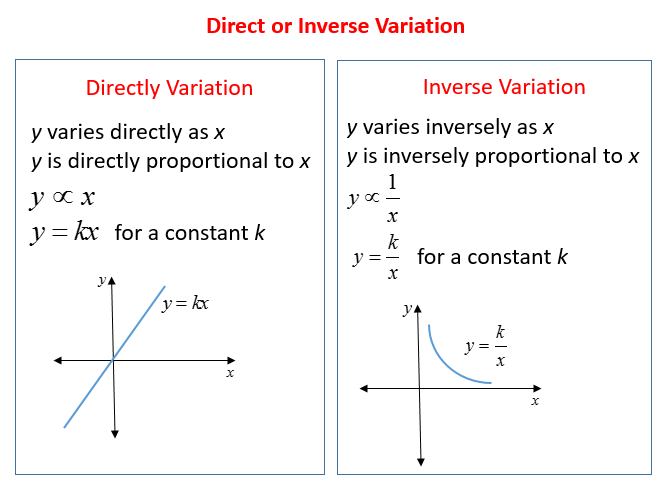



Direct Variation Video Lessons Examples And Solutions
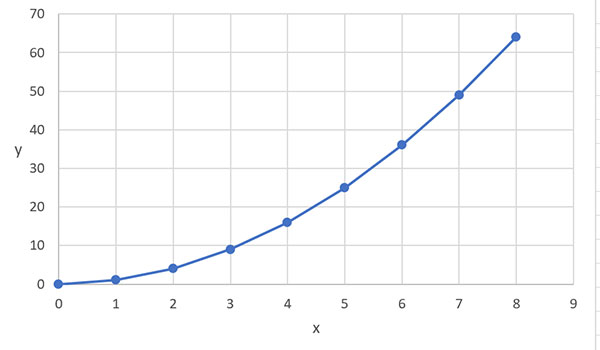



Mathematical Relationships Mathematical Relationships
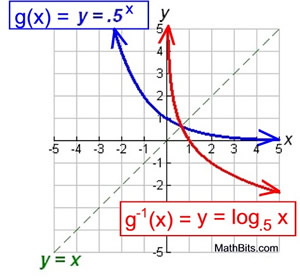



Exponential Functions Mathbitsnotebook Ccss Math
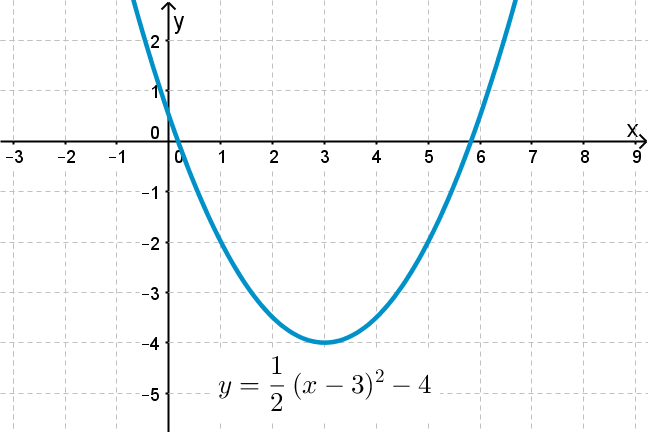



Scaling And Translating Quadratic Functions




Inversely Proportional Definition Formula Examples Video Lesson Transcript Study Com



1
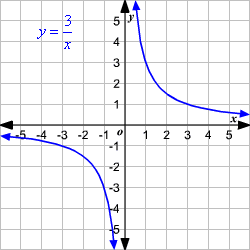



Inverse Variation




The Characteristics Of The Graph Of A Reciprocal Function Graphs And Functions And Simultaneous Equations




Graphing Square Root And Cubed Root Functions Ck 12 Foundation
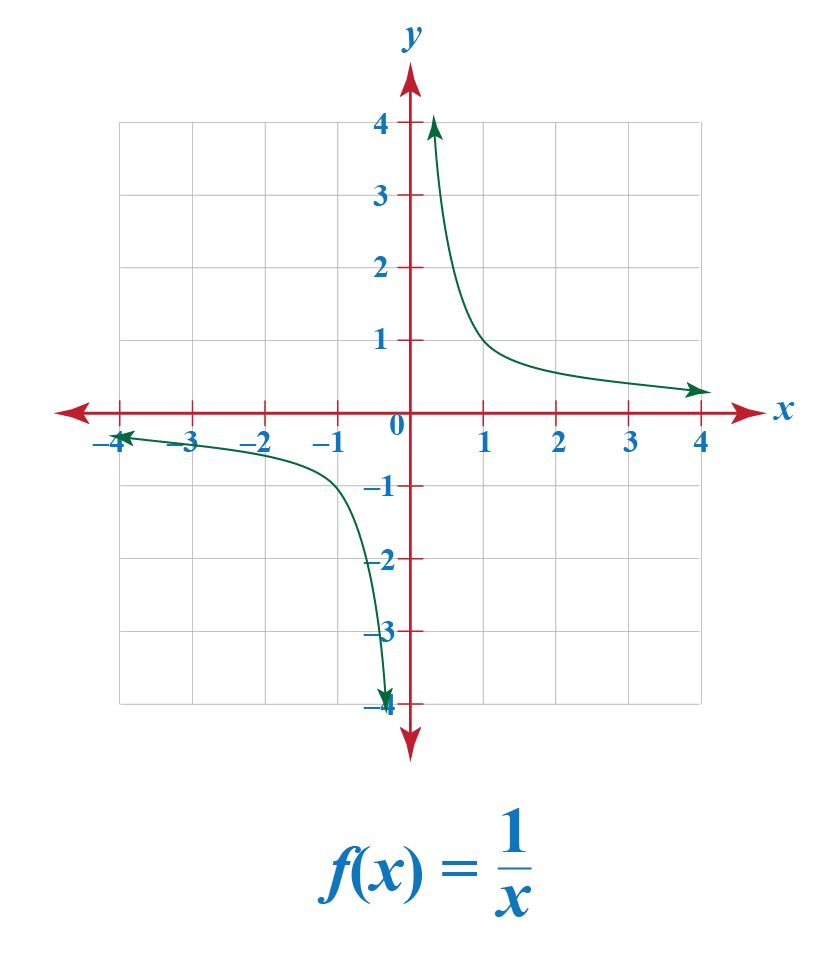



Reciprocal Functions Graphs Calculator Examples Cuemath
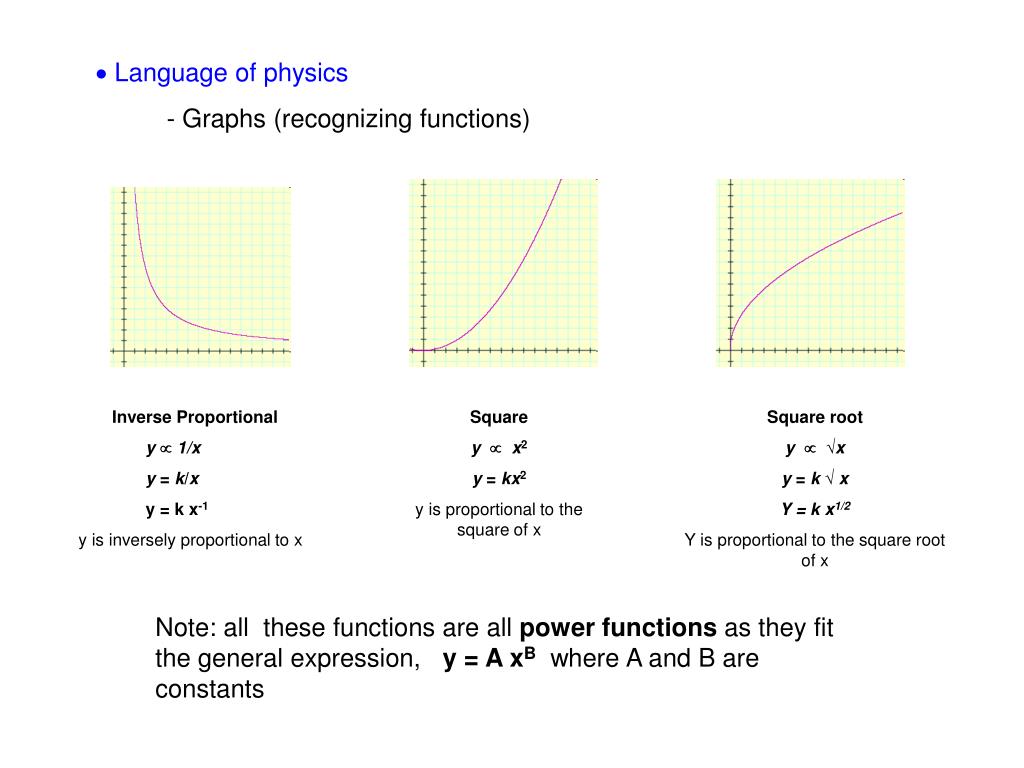



Ppt Pendulum Mock Lab Powerpoint Presentation Free Download Id




Variation




Honors Algebra 2 2nd Hour Fall 11 3 9 Variation



3
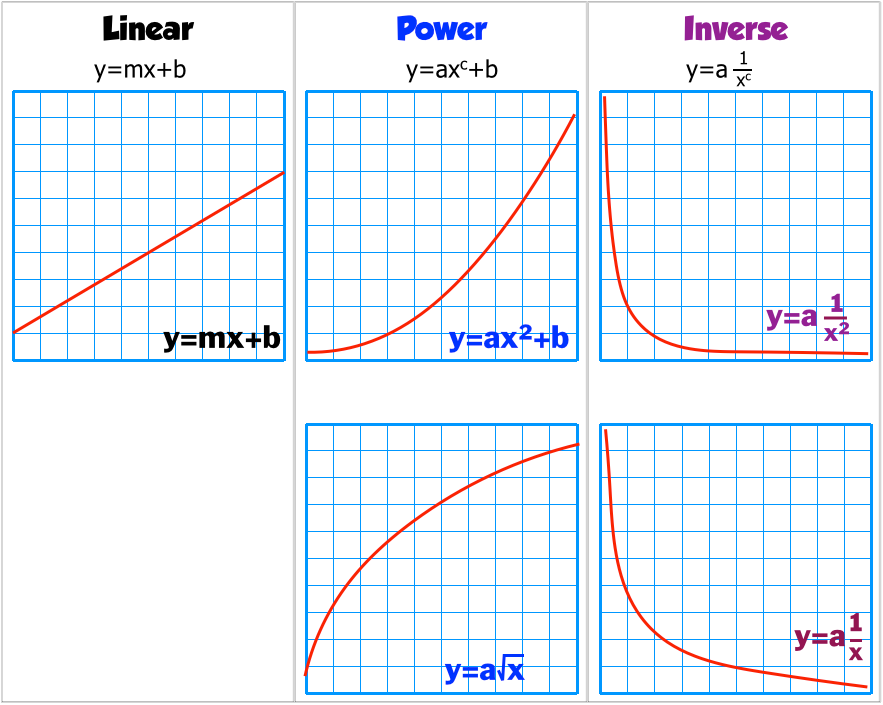



Linearizing Data
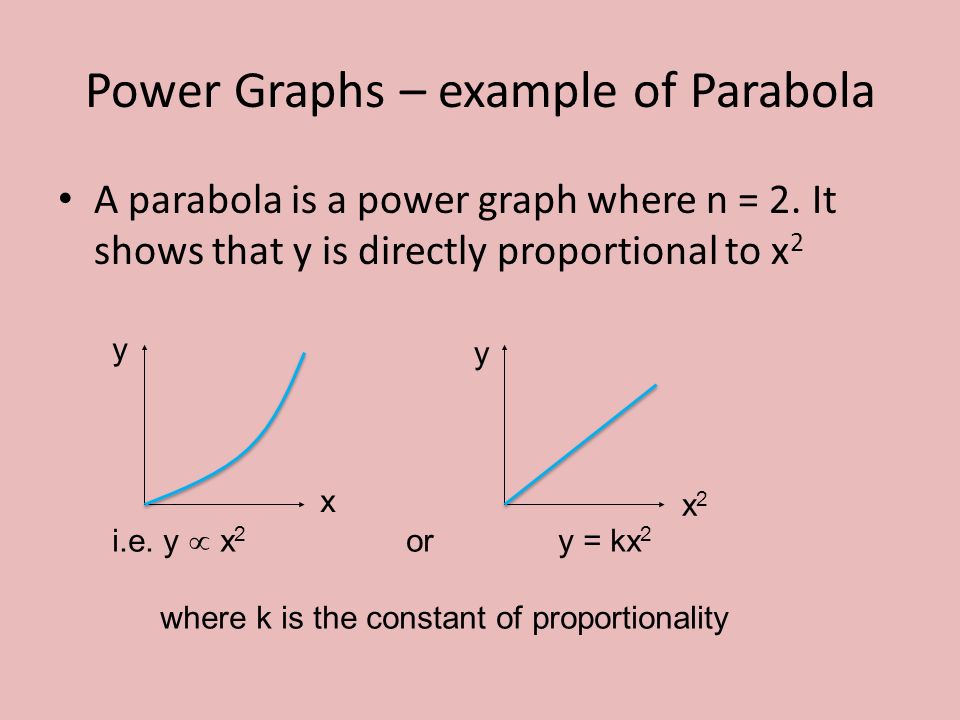



Proportional Techniques Standard Graphs Proportional Techniques Ppt Download



Reciprocal Function Explanation Construction Of Graph And Solved Examples
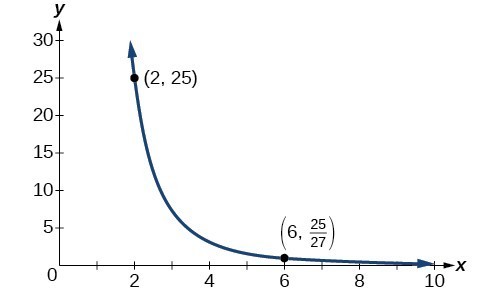



Inverse And Joint Variation College Algebra



Times Module M35 Proportion
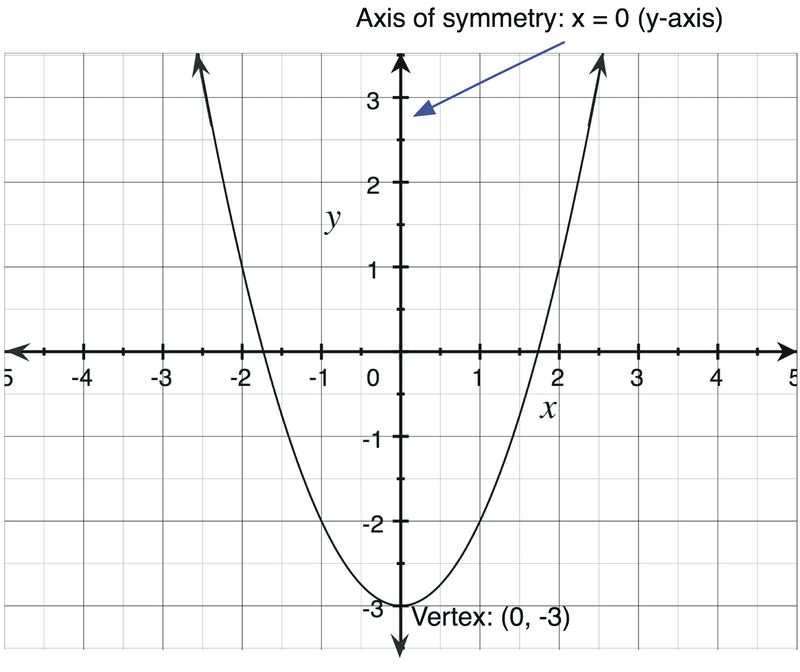



Square And Cube Function Families Read Algebra Ck 12 Foundation
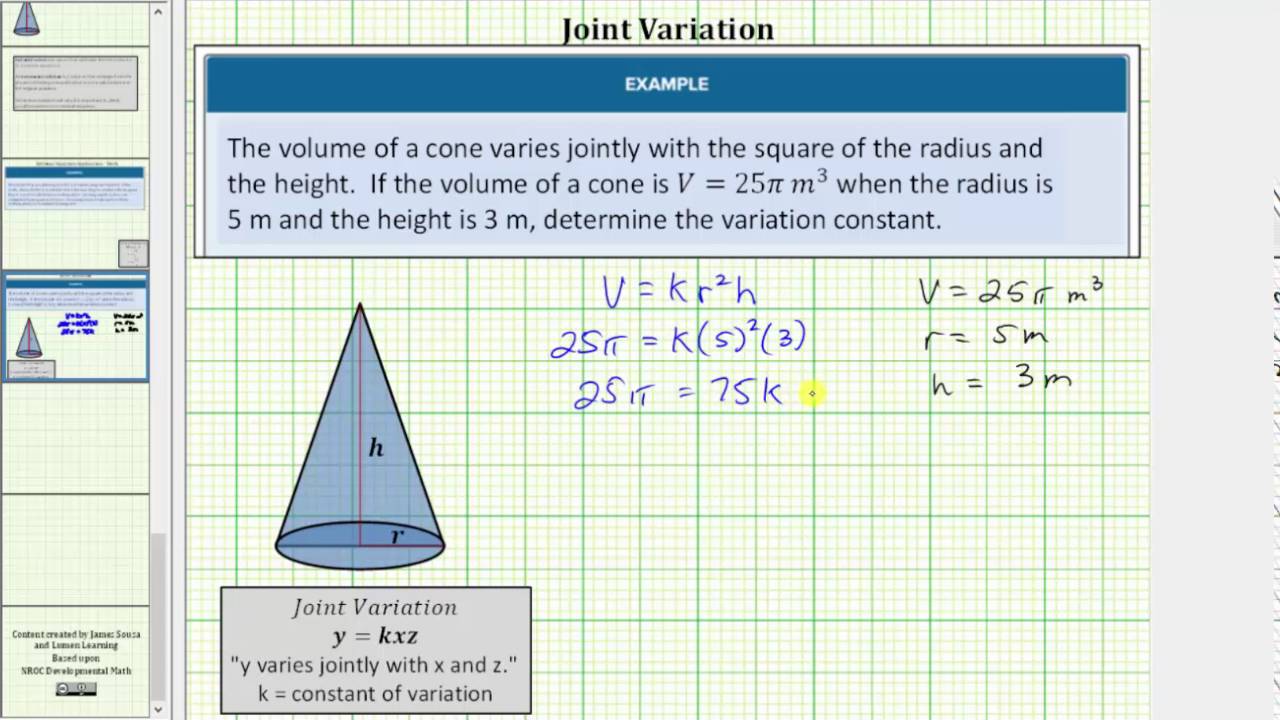



Inverse And Joint Variation College Algebra
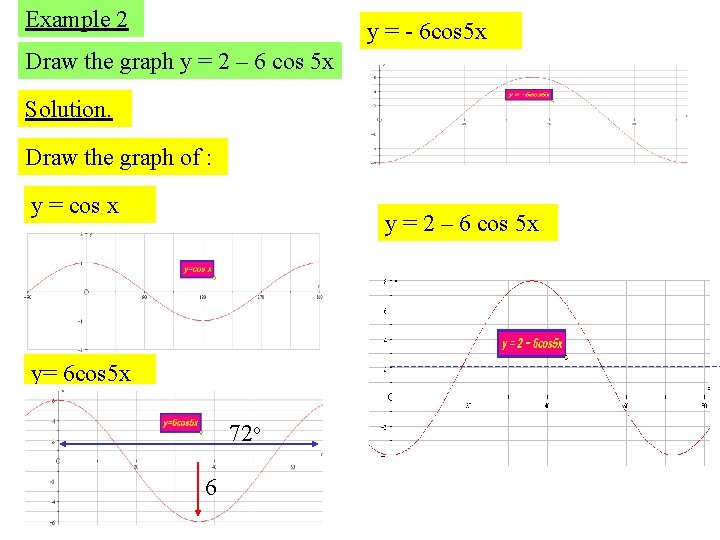



Drawing Trigonometric Graphs The Basic Graphs You Should



Integrated Rate Laws
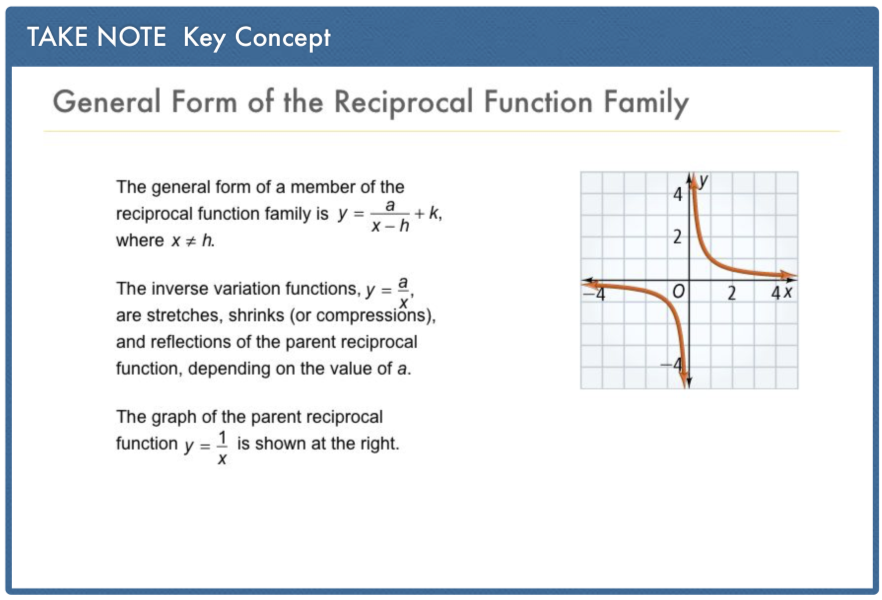



Algebra 2 8 2 Complete Lesson The Reciprocal Function Family Matthew Richardson Library Formative




Inversely Proportional Definition Formula Examples Video Lesson Transcript Study Com
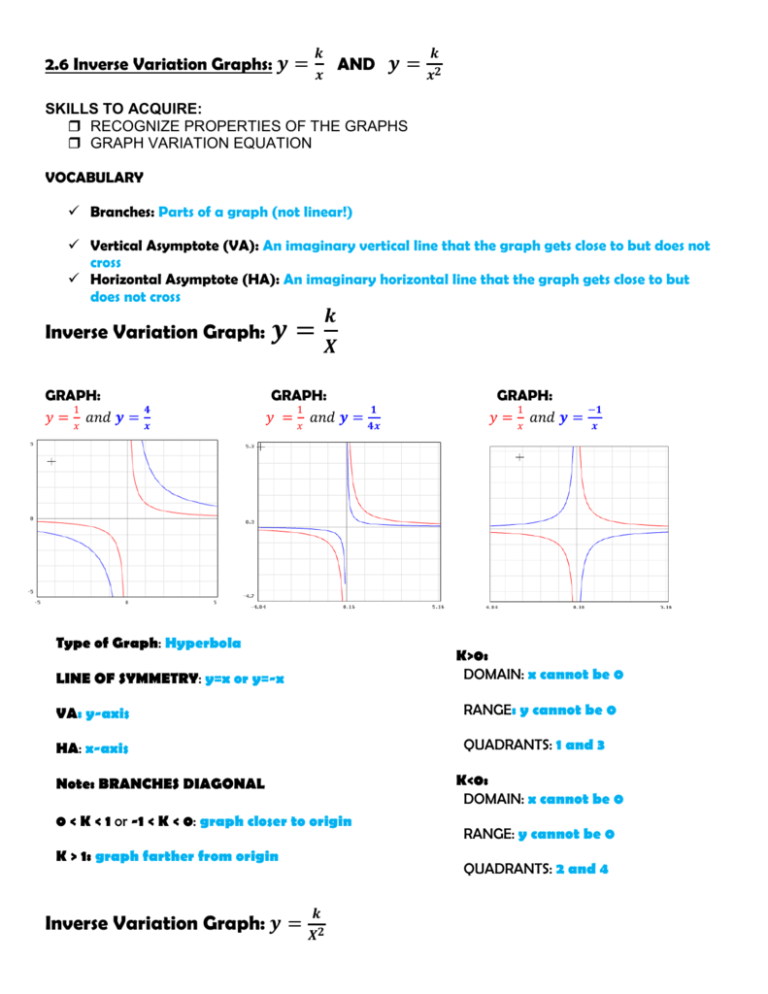



And Inverse Variation Graph Inverse Variation Graph



Www Brainfuse Com Jsp Alc Resource Jsp S Gre C Cc 10
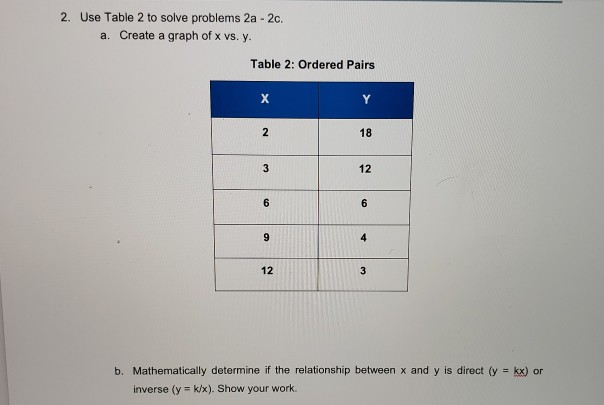



2 Use Table 2 To Solve Problems 2a 2c A Create A Chegg Com



2




Identifying Constant Of Proportionality Graphically Video Khan Academy



Graph Graph Equations With Step By Step Math Problem Solver




How To Draw Graph Of F X E X2 Quora
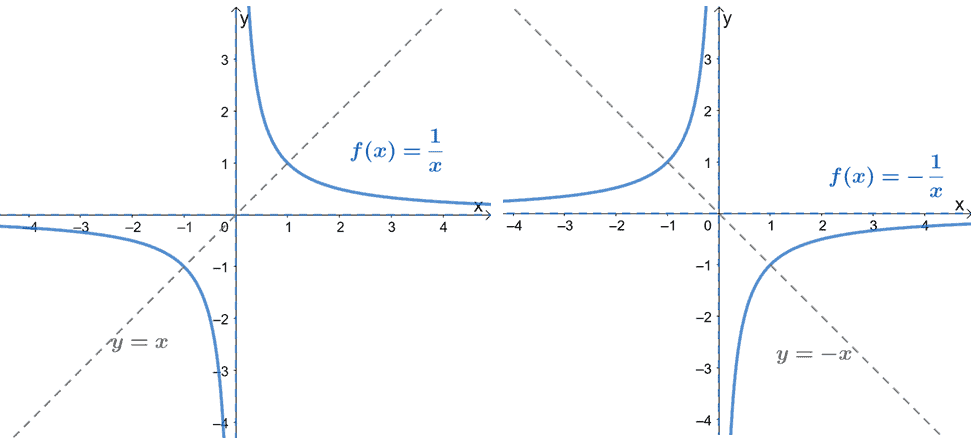



Reciprocal Function Properties Graph And Examples




Rational Functions Algebra And Trigonometry



1




Identifying Constant Of Proportionality Graphically Video Khan Academy




Parent Functions And Transformations She Loves Math




Quadratic Function Wikipedia




Variation
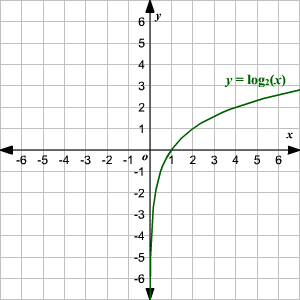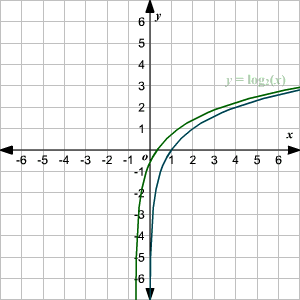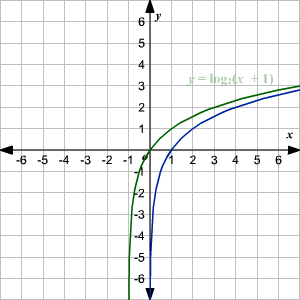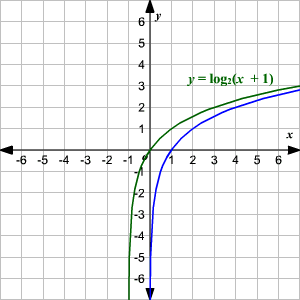



Graphing Logarithmic Functions
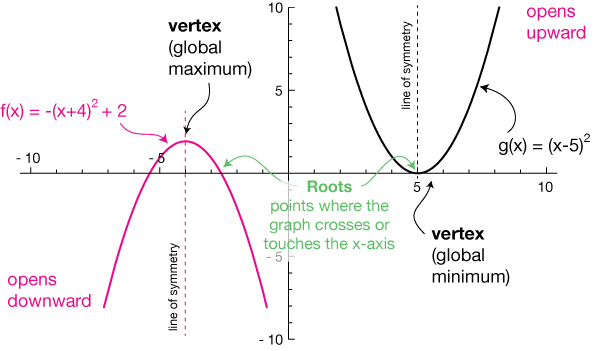



Quadratic Functions



Times Module M35 Proportion




4 Ways To Determine Whether Two Variables Are Directly Proportional




Test Algebra 1 Unit 13 Key Terms Quizlet



2fv5d843v9w22sxtto1ibxtu Wpengine Netdna Ssl Com Wp Content Uploads 15 12 Ratio H Direct Inverse Proportion V2 Solutions Pdf
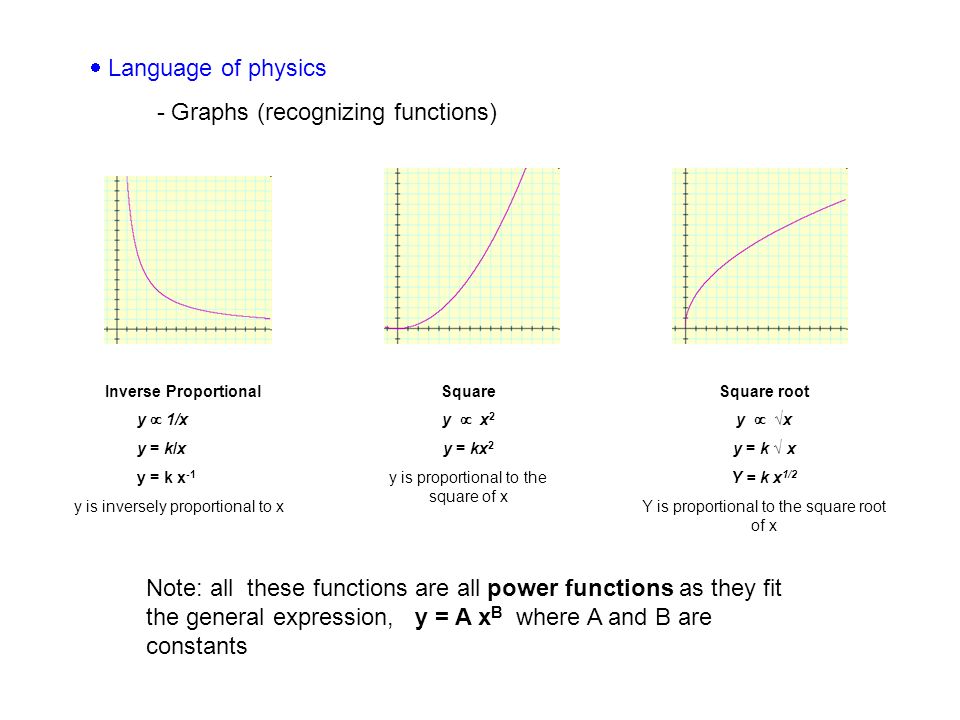



Pendulum Mock Lab Ppt Video Online Download




Y Proportional To X Squared Graph Novocom Top
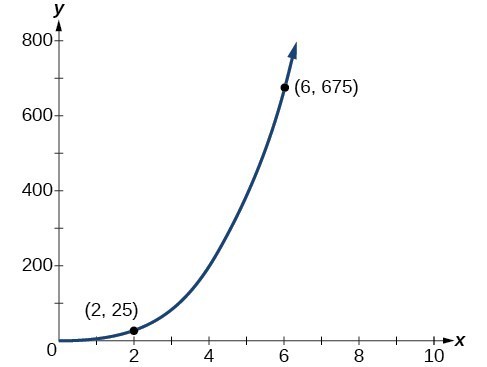



Variation College Algebra




Topic 1 Physics Physical Measurement
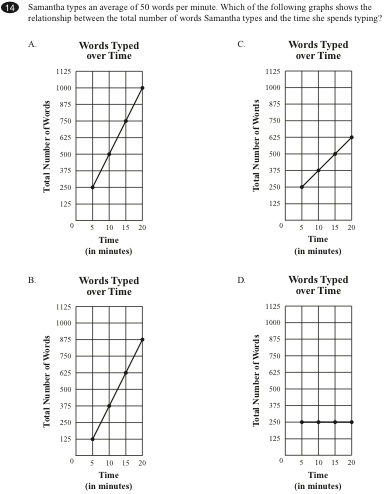



7 2 1 Proportional Relationships Minnesota Stem Teacher Center
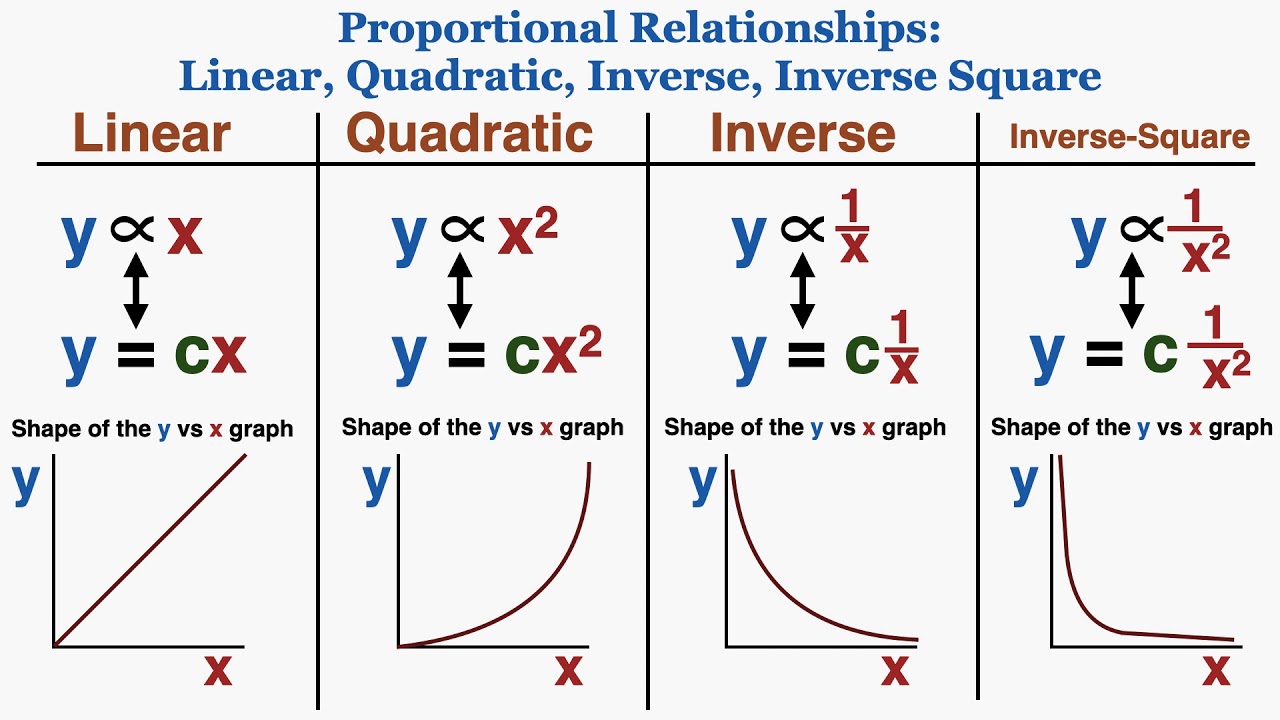



Using Linear Quadratic Inverse Inverse Square Graphs To Understand Proportionality Ib Physics Youtube



0 件のコメント:
コメントを投稿